- Sistem Koordinat Cartesius,
- Sistem Koordinat Kutub,
- Sistem Koordinat Tabung, dan
- Sistem Koordinat Bola.
Sistem koordinat Kartesius
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Dalam matematika, Sistem koordinat Kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut.
Untuk mendefinisikan koordinat diperlukan dua garis berarah yang tegak lurus satu sama lain (sumbu x dan sumbu y), dan panjang unit, yang dibuat tanda-tanda pada kedua sumbu tersebut (lihat Gambar 1).
Sistem koordinat Kartesius dapat pula digunakan pada dimensi-dimensi yang lebih tinggi, seperti 3 dimensi, dengan menggunakan tiga sumbu (sumbu x, y, dan z).
Dengan menggunakan sistem koordinat Kartesius, bentuk-bentuk geometri seperti kurva dapat diekspresikan dengan persamaan aljabar. Sebagai contoh, lingkaran yang berjari-jari 2 dapat diekspresikan dengan persamaan x² + y² = 4 (lihat Gambar 2).
Istilah Kartesius digunakan untuk mengenang ahli matematika sekaligus filsuf dari Perancis Descartes, yang perannya besar dalam menggabungkan aljabar dan geometri (Cartesius adalah latinisasi untuk Descartes). Hasil kerjanya sangat berpengaruh dalam perkembangan geometri analitik, kalkulus, dan kartografi.
Ide dasar sistem ini dikembangkan pada tahun 1637 dalam dua tulisan karya Descartes. Pada bagian kedua dari tulisannya Discourse on Method, ia memperkenalkan ide baru untuk menggambarkan posisi titik atau obyek pada sebuah permukaan, dengan mengggunakan dua sumbu yang bertegak lurus antar satu dengan yang lain. Dalam tulisannya yang lain, La Géométrie, ia memperdalam konsep-konsep yang telah dikembangkannya.
Lihat koordinat (matematika) untuk sistem-sistem koordinat lain seperti sistem koordinat polar.
Sistem koordinat dua dimensi
Sistem koordinat Kartesius dalam dua dimensi umumnya didefinisikan dengan dua sumbu yang saling bertegak lurus antar satu dengan yang lain, yang keduanya terletak pada satu bidang (bidang xy). Sumbu horizontal diberi label x, dan sumbu vertikal diberi label y. Pada sistem koordinat tiga dimensi, ditambahkan sumbu yang lain yang sering diberi label z. Sumbu-sumbu tersebut ortogonal antar satu dengan yang lain. (Satu sumbu dengan sumbu lain bertegak lurus.)
Titik pertemuan antara kedua sumbu, titik asal, umumnya diberi label 0. Setiap sumbu juga mempunyai besaran panjang unit, dan setiap panjang tersebut diberi tanda dan ini membentuk semacam grid. Untuk mendeskripsikan suatu titik tertentu dalam sistem koordinat dua dimensi, nilai x ditulis (absis), lalu diikuti dengan nilai y (ordinat). Dengan demikian, format yang dipakai selalu (x,y) dan urutannya tidak dibalik-balik.
Pilihan huruf-huruf didasari oleh konvensi, dimana huruf-huruf yang dekat akhir (seperti x dan y) digunakan untuk menandakan variabel dengan nilai yang tak diketahui, sedngakan huruf-huruf yang lebih dekat awal digunakan untuk menandakan nilai yang diketahui.
Sebagai contoh, pada Gambar 3, titik P berada pada koordinat (3,5).
Karena kedua sumbu bertegak lurus satu sama lain, bidang xy terbagi menjadi empat bagian yang disebut kuadran, yang pada Gambar 3 ditandai dengan angka I, II, III, dan IV. Menurut konvensi yang berlaku, keempat kuadran diurutkan mulai dari yang kanan atas (kuadran I), melingkar melawan arah jarum jam (lihat Gambar 3). Pada kuadran I, kedua koordinat (x dan y) bernilai positif. Pada kuadran II, koordinat x bernilai negatif dan koordinat y bernilai positif. Pada kuadran III, kedua koordinat bernilai negatif, dan pada kuadran IV, koordinat x bernilai positif dan y negatif (lihat tabel dibawah ini).
| Kuadran | nilai x | nilai y |
|---|---|---|
| I | > 0 | > 0 |
| II | <> | > 0 |
| III | <> | <> |
| IV | > 0 | <> |



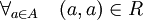




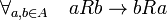




 bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku  dan
dan 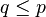 berarti
berarti