Untuk mendefinisikan fungsi dapat digunakan notasi berikut.
Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.
atau
Suatu fungsi dari himpunan A ke himpunan B adalah suatu relasi yang khusus, yaitu relasi yang setiap anggota A dipasangkan dengan tepat satu anggota B. Untuk fungsi dari A ke B diperlukan syarat, yaitu:
- mempunyai dua himpunan A dan B;
- suatu relasi yang menghubungkan setiap anggota A dengan tepat satu anggota B.

- Himpunan A disebut daerah asal atau daerah definisi atau domain fungsi itu. Himpunan B disebut daerah kawan atau kodomain dan himpunan semua anggota B yang dipasangkan dengan anggota A dinamakan daerah hasil atau daerah nilai ( range ) fungsi itu.
- Jika a anggota daerah asal, maka anggota daerah hasil yang bersesuaian dengan a disebut bayangan dari a ( peta dari a ) oleh fungsi f, dan dinyatakan dengan f(a). Himpunan semua bayangan membentuk daerah hasil fungsi tersebut. f(a) juga disebut nilai fungsi untuk a.
- Fungsi f yang ditentukan oleh rumus f(x)=ax+c dengan a, c ` R dan a g 0 dinamakan fungsi linear.
f(x) = ax + c adalah rumus fungsi linear.
y = ax + c adalah persamaan fungsi linear.
- Untuk persamaan fungsi y = ax + c, x disebut variabel bebas dan y disebut variabel tak bebas.
- Menggambar grafik fungsi
- Membuat daftar untuk menentukan daerah hasil.
- Menentukan himpunan pasangan berurutan.
- Membuat sumbu vertikal dan horizontal.
- Meletakkan noktah-noktah dari himpunan pasangan berurutan yang telah dibuat.
- Jika n(A) = p dan n(B) = q, maka banyaknya fungsi yang mungkin dari A ke B adalah q p .
- Himpunan A dan B dikatakan berkorespondensi satu-satu jika anggota-anggota himpunan A dan B dipasangkan sedemikian rupa sehingga setiap anggota himpunan A berpasangan dengan satu anggota himpunan B daqn setiap anggota himpunan B berpasangan dengan satu anggota himpunan A.

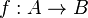



Tidak ada komentar:
Posting Komentar