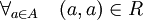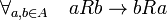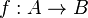WELCOME: 13 Jan 2010

Rabu, 13 Januari 2010

Relasi

Hubungan/relasi dari himpunan A ke himpunan B adalah suatu pemasangan anggota-anggota A dengan anggota-anggota B.

A. SEBUAH RELASI R TERDIRI DARI:

1.Himpunan A
2.Himpunan B
3.Sebuah kalimat terbuka P(x,y) yang menyatakan hubungan antara himpunan A dengan himpunan B.
Dimana x bersesuaian dengan a Î A dengan y bersesuaian
denganb Î B.
- Bila P(a,b) betul maka a berelasi dengan b. Ditulis a R b
- Bila tidak demikian maka a R b

B. CARA-CARA MENYATAKAN RELASI :

1. Dengan Himpunan Pasangan Berurutan.
2. Dengan Diagram Panah.
3. Dengan Diagram Cartesius.

1. Himpunan Pasangan Berurutan
...Himpunan yang anggotanya semua pasangan berurutan (x,y) dinamakan himpunan pasangan berurutan.
R = {(2,4), (2,6), (3,3), (3,6), (4,4)}

Contoh :
Via: aku senang permen dan coklat
Andre: aku senang coklat dan es krim
Ita: aku suka es krim

Dari contoh di atas dapat dibuat dua himpunan, yaitu :
-Himpunan A adalah himpunan nama orang
A = { Via, Andre, Ita }
-Himpunan B adalah himpunan makanan kesukaan
B = { es krim, coklat, permen }

2. Diagram Panah
Langkah-langkah cara menyatakan relasi dengan diagram panah:
- Membuat dua lingkaran atau ellips.
- Untuk meletakkan anggota himpunan A dan anggota himpunan B x=A diletakkan pada lingkaran A dan y=B diletakkan pada lingkaran B.
- x dan y dihubungkan dengan anak panah.
- Arah anak panah menunjukkan arah relasi.
- Anak panah tersebut mewakili aturan relasi.
- bila R adalah sebuah relasi, maka himpunan dari relasi ini adalah:
R = {(a,b) ½ a Î A; b Î B; P(a,b) adalah betul}
Ket: Jika A=B, maka P(x,y) mendefinisikan sebuah relasi
di dalam A.

contoh :

R = (A,B, P(x,y))
A = {2,3,4}
B = {3,4,5,6}
P(x,y) menyatakan x pembagi y

3. Diagram Cartesius
Pada diagram cartesius diperlukan dua salib sumbu yaitu; sumbu mendatar (horisontal) dan sumbu tegak (vertikal) yang berpotongan tegak lurus.
1. x=A diletakkan pada sumbu mendatar.
2. y=B diletakkan pada sumbu tegak.
3. Pemasangan (x,y) ditandai dengan sebuah noktah yang koordinatnya ditulis sebagai pasangan berurutan (x,y).

4. Kalimat Terbuka P (x,y)

Relasi A x A

Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:

Refleksif
Irefleksif
Simetrik
Anti-simetrik
Transitif

Kita menyebut relasi R dari A kepada A sebagai relasi R dalam A.

Relasi Refleksif

Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen A berhubungan dengan dengan dirinya sendiri.

$\forall_{a \in A}\quad (a,a) \in R$

atau

$\forall_{a \in A}\quad a R a$

Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan x dan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.

Relasi Irefleksif

Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.

$\forall_{a \in A}\quad (a,a) \notin R$

atau

$\forall_{a \in A}\quad \lnot(a R a)$

Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.

Contoh lain dalam himpunan bilangan bulat adalah, relasi <> adalah irefleksif.

Relasi Simetrik

Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota A berhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.

$\forall_{a, b \in A}\quad (a,b) \in R \rightarrow (b,a) \in R$

atau

$\forall_{a, b \in A}\quad a R b \rightarrow b R a$

Sebuah relasi “ $x + y$ genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.

Relasi Anti-simetrik

Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsi a dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.

$\forall_{a, b \in A}\quad a \neq b \rightarrow ((a,b) \in R \rightarrow (b,a) \notin R)$

atau

$\forall_{a, b \in A}\quad a \neq b \rightarrow (a R b \rightarrow \lnot (b R a))$

Dalam kebanyakan literatur biasanya ditulis sebagai kontraposisinya seperti di bawah ini. Keuntungan bentuk ini adalah tidak mengandung negasi, dan hanya mengandung satu implikasi.

$\forall_{a, b \in A}\quad (a,b) \in R \wedge (b,a) \in R \rightarrow a=b$

atau

$\forall_{a, b \in A}\quad a R b \wedge b R a \rightarrow a=b$

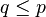Relasi $\leq$ bersifat anti-simetrik, karena $5 \leq 6$ mengakibatkan $\lnot (6 \leq 5)$ . Demikian juga jika ada p dan q yang terhadap mereka berlaku $p \leq q$ dan $q \leq p$ berarti $p = q$ .

Relasi Transitif

Sebuah (a,b) \in R \wedge (bin R \rightarrow (a,c) \in R atau

Gagal memparse (fungsi yang tidak diketahui\berhubungan): \forall<>\forall_{a, b, c \in A}\q_{a,relasi d b, dengac \in A}\quad a R''b'', dan b \wedge b R c \rightarrow a R c

Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 <>

Relasi khusus

Relasi Ekivalen

Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:

Refleksif
Simetrik, dan
Transitif

Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.

Orde Parsial

Orde parsial adalah relasi yang bersifat:

Refleksif
Anti-simetrik, dan
Transitif

Lihat pula

Definisi Fungsi

Fungsi adalah relasi yang menghubungkan setiap domain dengan kodomain.

Untuk mendefinisikan fungsi dapat digunakan notasi berikut.

$f : A \rightarrow B$

Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.

$x \in A$

$f : x \rightarrow x^2$

atau

$f(x) =\, x^2$

Suatu fungsi dari himpunan A ke himpunan B adalah suatu relasi yang khusus, yaitu relasi yang setiap anggota A dipasangkan dengan tepat satu anggota B. Untuk fungsi dari A ke B diperlukan syarat, yaitu:

mempunyai dua himpunan A dan B;
suatu relasi yang menghubungkan setiap anggota A dengan tepat satu anggota B.

Himpunan A disebut daerah asal atau daerah definisi atau domain fungsi itu. Himpunan B disebut daerah kawan atau kodomain dan himpunan semua anggota B yang dipasangkan dengan anggota A dinamakan daerah hasil atau daerah nilai ( range ) fungsi itu.
Jika a anggota daerah asal, maka anggota daerah hasil yang bersesuaian dengan a disebut bayangan dari a ( peta dari a ) oleh fungsi f, dan dinyatakan dengan f(a). Himpunan semua bayangan membentuk daerah hasil fungsi tersebut. f(a) juga disebut nilai fungsi untuk a.
Fungsi f yang ditentukan oleh rumus f(x)=ax+c dengan a, c ` R dan a g 0 dinamakan fungsi linear.

f(x) = ax + c adalah rumus fungsi linear.

y = ax + c adalah persamaan fungsi linear.

Untuk persamaan fungsi y = ax + c, x disebut variabel bebas dan y disebut variabel tak bebas.
Menggambar grafik fungsi

Membuat daftar untuk menentukan daerah hasil.
Menentukan himpunan pasangan berurutan.
Membuat sumbu vertikal dan horizontal.
Meletakkan noktah-noktah dari himpunan pasangan berurutan yang telah dibuat.

Jika n(A) = p dan n(B) = q, maka banyaknya fungsi yang mungkin dari A ke B adalah q ^p .
Himpunan A dan B dikatakan berkorespondensi satu-satu jika anggota-anggota himpunan A dan B dipasangkan sedemikian rupa sehingga setiap anggota himpunan A berpasangan dengan satu anggota himpunan B daqn setiap anggota himpunan B berpasangan dengan satu anggota himpunan A.

Jenis-Jenis Fungsi

1) Fungsi konstan (fungsi tetap)

Fungsi konstan adalah fungsi f yang dinyatakan dalam rumus f(x) = c, dengan c suatu
konstanta. Grafiknya jika dilukis dalam suatu sumbu koordinat dimana domainnya
sumbu x merupakan garis yang sejajar dengan sumbu x.

2) Fungsi linear

A. Pengertian fungsi linier
Fungsi linier adalah suatu fungsi yang variabelnya berpangkat satu atau suatu fungsi
yang grafiknya merupakan garis lurus. Oleh karena itu fungsi linier sering disebut
dengan persamaan garis lurus (pgl) dengan bentuk umumnya sbb.:
f : x → mx + c atau f(x) = mx + c atau y = mx + c
m adalah gradien / kemiringan / kecondongan dan c adalah konstanta

B. Melukis grafik fungsi linier
Langkah-langkah melukis grafik fungsi linier
a Tentukan titik potong dengan sumbu x, y = 0 diperoleh koordinat A( x1, 0)
b Tentukan titik potong dengan sumbu y, x = 0 diperoleh koordinat B( 0, y1)
c hubungkan dua titik A dan B sehingga terbentuk garis lurus

C. Gradien dan persamaan garis lurus
a. Garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) memiliki gradien m:
m = y1-y2 atau m = y2-y1
x1-x2 x2-x1

b. Persamaan garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) adalah:
y-y1 = x-x1
y2-y1 x2-x1

c. Persamaan garis lurus (pgl) yang bergradien m dan melalui titik A(x1, y1) adalah:
y = m (x – x1 ) + y1

D. Menentukan gradien dari persamaan garis lurus (pgl)
- Persamaan garis lurus : ax + by = c maka gradiennya m = - a/b
- Persamaan garis lurus : y = ax + b maka m = a
- Garis yang sejajar sumbu x memiliki persamaan y = c dan m = 0
- Garis yang sejajar sumbu y memiliki persamaan x = c dan tidak memiliki gradient

E. Titik potong dua buah garis
Menentukan titik potong dua buah garis lurus identik dengan menyelesaikan
penyelesaian sistem persamaan linier dua variabel baik dengan metode eleminiasi,
metode substitusi maupun metode grafik

F. Hubungan dua buah garis
Dua garis yang bergradien m1 dan m2 dikatakan sejajar jika m1 = m2 dan tegak lurus jika m1 x m2 = -1

3) Fungsi kuadrat
Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh
f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan
grafiknya berupa parabola.

4) Fungsi identitas
Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi
berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri.
Grafik fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik
absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x.

5) Fungsi tangga (bertingkat)
Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk
interval-interval yang sejajar.

6) Fungsi modulus
Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan
setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.

7) Fungsi ganjil dan fungsi genap
Suatu fungsi f(x) disebut fungsi ganjil apabila berlaku f(–x) = –f(x) dan disebut
fungsi genap apabila berlaku f(–x) = f(x). Jika f(–x) ≠ –f(x) maka fungsi ini
tidak genap dan tidak ganjil.

8. Fungsi Polinomial
Fungsi Polinomial adalah fungsi f yang dinyatakan dalam bentuk :
f(x) = an x n + an-1 x n-1 + ……. A2 x 2 + a1 x a0
Jika n = 1 maka terbentuk fungsi linier (grafiknya berbentuk garis lurus).
Jika n = 2 maka terbentuk fungsi kuadrat( grafiknya berbentuk parabola).

Fungsi Kuadrat dan Fungsi Invers

Fungsi Kuadarat

Bentuk umum fungsi kuadrat adalah: f(x) = ax2 + bx + c dimana a, b, c bilangan real dan
a ≠ 0. Grafik fungsi kuadrat berbentuk parabola dengan persamaan y = ax2 + bx + c.
Beberapa langkah yang ditempuh untuk menggambar grafik fungsi kuadrat adalah:

a. Titik potong grafik dengan sumbu x, dengan mengambil y = 0

b. Titik potong grafik dengan sumbu y, dengan mengambil x = 0

c. Sumbu simetri grafik yaitu x = - b
2a

d. Koordinat titik balik /titik puncak (x,y) di mana x = - b dan y = - D
2a 4a

dengan D = b2 – 4ac.

e. Grafik terbuka ke bawah jika a <> 0.

1). Kedudukan Grafik fungsi kuadrat

Kedudukan grafik fungsi kuadrat yang dilihat dari banyaknya titik potong dengan
sumbu x, ditentukan oleh nilai diskriminan yaitu D = b2 – 4ac. Sedangkan grafik membuka ke atas atau ke bawah ditentukan oleh tanda a (koefisien x2).

Kedudukan grafik fungsi kuadrat ditinjau dari nilai diskriminan ( D ) dan a adalah
sebagai berikut:
a. Jika D > 0 maka grafik memotong sumbu x di dua titik
b. Jika D = 0 maka grafik menyinggung sumbu x
c. Jika D <> 0 maka grafik terbuka ke atas dan diperoleh titik puncak minimum

Jika a <>

2) Menentukan Persamaan Grafik Fungsi Kuadrat

Persamaan grafik fungsi kuadrat dapat dicari jika kondisi-kondisi dibawah ini diketahui:
a. Grafik memotong sumbu x di (x¬1,0) dan (x2,0) serta melalui titik sembarang (x3,y3) pada grafik, maka persamaanya adalah y = a(x – x1)(x – x2).
b. Grafik mempunyai titik balik P(xp,yp) serta melalui titik sembarang (x1,y1) pada grafik, maka persamaanya adalah y = a(x – xp)2 + yp.
c. Grafik melalui tiga buah titik yaitu (x1,y1), (x2,y2) dan (x3,y3), maka persamaanya adalah y = ax2 + bx + c.

Fungsi Invers

1. Syarat agar Suatu Fungsi Mempunyai Invers
Semua himpunan yang dipetakan oleh fungsi mempunyai invers. Invers dari himpunan
tersebut dapat berupa fungsi atau bukan fungsi.

Jika fungsi f = A→B dinyatakan dengan pasangan terurut f = {(a, b) | a A dan b B}
maka invers fungsi f adalah f -1= b→A ditentukan oleh f -1= {(b, a) | b B, dan a A}.

2. Menentukan Aturan Fungsi Invers dari Suatu Fungsi
Suatu fungsi f akan mempunyai invers, yaitu f –1 jika dan hanya jika fungsi f bijektif
atau dalam korespondensi satu-satu. Misalkan, f merupakan fungsi dari A ke B, maka
f –1 merupakan fungsi invers f jika berlaku (f -1. f)(x) = x dan (f . f -1)(x) = x.

Untuk menentukan fungsi invers dari suatu fungsi dapat dilakukan dengan cara
berikut ini.
a. Buatlah permisalan f(x) = y pada persamaan.
b. Persamaan tersebut disesuaikan dengan f(x) = y, sehingga ditemukan fungsi dalam
y dan nyatakanlah x = f(y).
c. Gantilah y dengan x, sehingga f(y) = f -1(x).

3. Kaitan Sifat Fungsi Invers dengan Fungsi Komposisi
Komposisi fungsi adalah penggolongan beberapa fungsi menjadi sebuah fungsi

Jika terdapat fungsi komposisi (g . f), maka (g . f) dapat dipandang sebagai suatu fungsi tunggal, sehingga pada fungsi tersebut dapat dicari inversnya.

Fungsi invers dari fungsi komposisi
Bila suatu fungsi h : A → C ditentukan oleh h = g . f dengan f : A → B dan
g : B → C maka fungsi invers dari fungsi komposisi adalah h-1= (g . f) -1.

Sifat-sifat fungsi invers dari fungsi komposisi:
1) (g . f) -1 (x) = (f -1 . g -1)(x)
2) (f . g) -1 (x) = (g -1 . f -1)(x)

Gradien

Bisi kita artikan Gradien/slope adalah nilai peubah “change value” antara 2 buah titik yang berbeda $a=(x_{0},y_{0})$ dan $b=(x_{1},y_{1})$ yang didefinisikan

$m_{a,b}=\frac{x_{1}-x_{0}}{y_{1}-y_{0}}$

Kenapa harus 2 buah titik yang berbeda? karena jika $a=b$ maka

$m_{a,b}=0/0$ . Dari gradien ini kita bisa membentuk persamaan garis lurus yang melalui $a$ dan $b$ dengan rumus sebagai berikut

$y-y_{0}=m_{a,b}(x-x_{0})$

Misalkan kita mempunyai suatu fungsi $f(x)$ dan $x_{0},x_{1}\in D(f(X))$ domain $f(x)$ maka kita mempunyai $f(x_{0}),f(x_{1})\in Im(f(x))$ image/daerah hasil $f(x)$ , sekarang kita mempunyai 2 buah titik yang berbeda $p=(x_{0},f(x_{0}))$ dan $q=(x_{1},f(x_{1}))$ , maka persamaan garis lurus yang menghubungkan $p$ dan $q$ kita sebut sebagai tali busur/secant line.

***

Sekarang kita asumsikan jarak $p$ dan $q$ sangat-sangat dekat sekali $\left\Vert p-q\right\Vert =h\rightarrow0$ atau dengan kata lain $p=(x_{o},f(x_{o}))$ dan $q=(x_{o}+h,f(x_{o}+h))$ , karen $h$ menuju nol tapi tidak pernah mencapai nol ( $h\neq0$ ) maka $p$ dan $q$ akan selalu menjadi 2 buah titik yang berbeda, tidak pernah sama, diperoleh gradien sebagai berikut

$m_{p,q}=\lim_{h\rightarrow0}\frac{f(x_{0}+h)-f(x_{0})}{x_{0}+h-x_{0}}$

$m_{p,q}=\lim_{h\rightarrow0}\frac{f(x_{0}+h)-f(x_{0})}{h}$

Inilah yang kita namakan turunan/derivative $f'(x_{0})$ , jadi turunan adalah gradien 2 buah titik pada kurva yang mana jarak keduanya sangat-sangat dekat sekali.